positionner selon un cercle¶

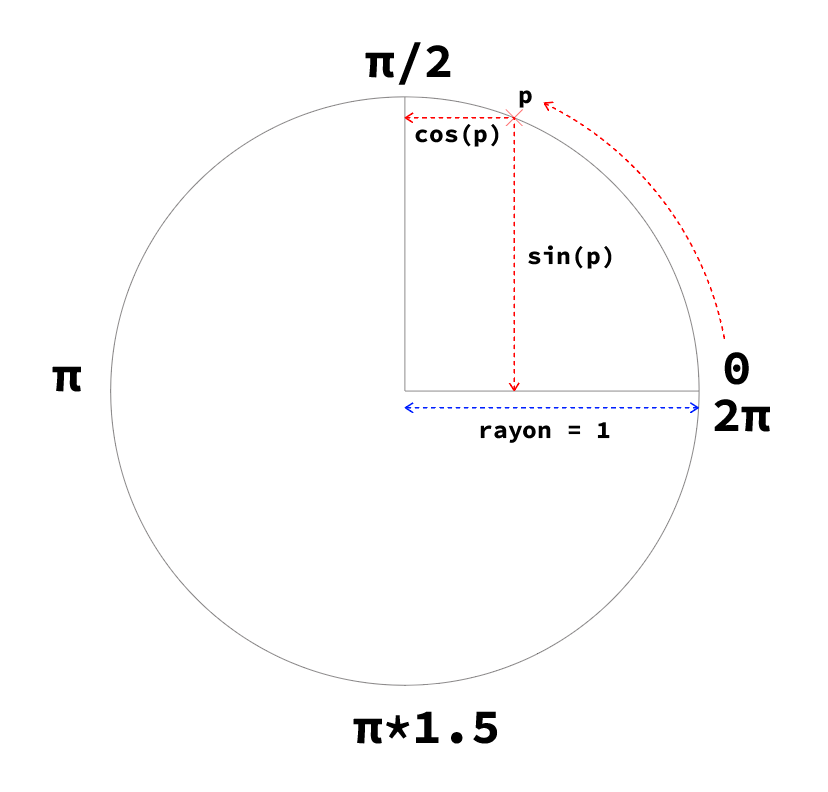
pour calculer la position d’un point sur un cercle de rayon 1
à partir de sa position sur le cercle (définie par la distance p parcourue sur le périmètre)
on calcule sa position en x cos(p)
on calcule sa position en y sin(p)
pour obtenir l’équivalent pour un cercle de périmètre r, on multiplie le résultat par r

exemples¶

Élément mobile selon un cercle de rayon 100¶

var x = transform.position[0] + Math.sin ( 2*Math.PI * ( time / thisComp.duration ) ) * 100;
var y = transform.position[1] + Math.cos ( 2*Math.PI * ( time / thisComp.duration ) ) * 100;

[x,y]

/* on récupère la position en x et y
de notre élément avant l'exécution
de l'expression */
var x_au_depart = transform.position[0];
var y_au_depart = transform.position[1];

// le tour du cercle = 2π
var tour_du_cercle = 2 * Math.PI;

// durée de la composition
var duree_composition = thisComp.duration;

// durée écoulée ramenée de 0 (0%) à 1 (100%)
var duree_ecoulee = time / duree_composition;

/* le sinus du tour du cercle
ramenée à la durée de la composition écoulée
= de 0 à 1,
multiplié par 100 = de 0 à 100 */
var x_cercle = Math.sin ( tour_du_cercle * duree_ecoulee ) * 100;
var y_cercle = Math.cos ( tour_du_cercle * duree_ecoulee ) * 100;

// on ajoute les coordonnées du cercle à celles de départ
var x = x_au_depart + x_cercle;
var y = y_au_depart + y_cercle;

[x,y]

Éléments multiples placés le long d’un cercle¶

var x = transform.position[0] + Math.sin ( index * Math.PI / 2.5) * 200;
var y = transform.position[1] + Math.cos ( index * Math.PI / 2.5) * 200;

[x,y]